|
Stelling van Pythagorasxml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />
De stelling van Pythagoras is waarschijnlijk de bekendste stelling in de wiskunde. De stelling dankt zijn naam aan de Griekse wiskundige Pythagoras. 'Zijn' stelling was overigens alleen maar nieuw voor de Grieken. In Soemerië was het resultaat al veel langer bekend, net als in Babelonië. Belangrijker nog dan de kennis van de stelling was het leveren van een bewijs daarvoor; daarbij waren de Grieken (Pythagoras of een van zijn leerlingen) wel de eersten.
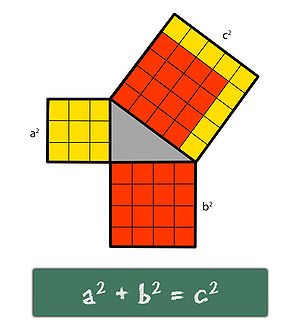
De stelling van Pythagoras luidt:
"In een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa (schuine zijde) gelijk aan de som van de kwadraten van de lengtes van de rechthoekszijden."
In wiskundige vorm:
Een paar bewijzen:
· Bewijs door geloofwaardigheid: Het klinkt goed, dus het moet waar zijn.
· Bewijs voor het gemak: Het zou heel mooi zijn als het waar is
· Bewijs door de verbeelding: We doen gewoon of het waar is.
· Bewijs door noodzakelijkheid: Het is beter dat het waar is, anders brokkelt de hele structuur van de wiskunde af.
· Bewijs door intimidatie: Doe niet zo stom! Natuurlijk is het waar!
· Bewijs per definitie: We definiëren dat het waar is.
· Bewijs door Godslastering: (Voorbeeld weggelaten)
· Bewijs door plagiaat: Op blz 289
.
· Bewijs door Mumbo Jumbo......... wat een nachtmerrie
· Bewijs door gebrek aan belangstelling: Wie kan het wat schelen?
· Bewijs door een verloren referentie: Ik weet dat ik het ergens heb zien staan
· Bewijs door analyse: Dit bewijs vereist analyse, dus dit slaan we maar over.
· Bewijs door intuïtie: ik heb het gevoel dat
· Bewijs door het ontwerp: Als het niet waar is, dan moet er een nieuw ontwerp bedacht worden waarin het waar wordt.
· Bewijs door onleesbaarheid: blablablablabla
· Bewijs door bladvulling: Dit bewijs is het zelfde als het laatste.
· Bewijs door het Goddelijk woord: En de Heer zei: Laat het waar zijn, en het was waar.
· Bewijs door koppigheid: Het kan me niet schelen wat je zegt. Het is waar
· Bewijs door vereenvoudiging: Dit bewijs is teruggebracht tot de verklaring van 1 + 1 = 2
· Bewijs door smeekbede: Oh alsjeblieft, laat het waar zijn!.
|
jij komt toch OOK niet uit het onderwijs zeker ? ik zit nu al heel mijn leven met complexen 
en nu jij nog met die stelling ! ( ik kom uit de zorgsector en die hebben geen wiskunde knobbel )
maar ik heb andere gaven 
